This was an old post in 2019, when I temporarily revived my interest in image generation with fractals. Like many long posts of that time, it was left unfinished and left dusting in the metaphysical corner.
With a renewed interest and the recently added table of content support, here is the finished version.
Iterative Function System
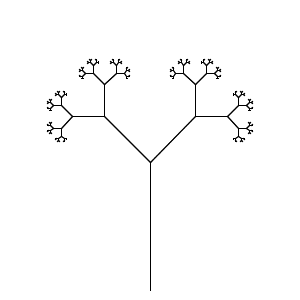
Back then when I was a kid, learning programming in LOGO language for fun, one of the biggest thing to learn was recursion. As recursion was a tricky topic for eight-year-olds, the tutorials focused in using the graph-drawing functionalities to illustrate how recursions worked.
For example, one of the way to illustrate what is a deep-first traversal of a binary tree is to actually draw such a tree in the same process.
And, more aesthetically pleasing examples such as the dragon curve.
There is not only the obvious self-similarity between the whole and the parts, but also the progressive similarity that each iteration step seems to be a “refinement” of the previous one. And the two similarities can be united when we formally describe such a fractal as an Iterated Function System. That is, we designate a series of transformations \(f_1, f_2, \dots, f_N\), and ask for a non-empty point set \(S\) so that
$$
S=\bigcup_{i=1}^N f_i(S).
$$
The “one step” operator \(S’=\bigcup_{i=1}^N f_i(S)\) is called the Hutchinson operator, and the \(S\) we are looking for is the non-empty fixed point of said operator.
\(S\) exists if either all \(f_1, f_2, \dots, f_N\) are contractive, or you are lucky. Mathematicians would definitively prefer the former condition. However, it might also be a great loss of diversity if we always stay in the safe zone!
Needless to say, it is easy to imagine that, from any non-empty set \(S_0\), we could use an iterative process to find an approximation to \(S\):
$$
S_i=\bigcup_{j=1}^N f_j(S_{i-1})
$$
Such an iterative definition, I believe, is where the name “Iterative Function System” comes from. Some people still limit the name to either affine transformations, contractive transformations, or, affine contractive transformations. And call everything else “generalized IFS”. I see little point in reserving the short name for the most boring variety, however, and I will use the term in its broadest sense.
While we have such an iterative definition, there is little practicality in representing \(S_M\) programatically, however, which has a cardinality of at most \(|S_0|\cdot N^M\), and betting on it having many coinciding points is hopeless as well. It is evident that some more approximation must be used.
The Chaos Game
The standard approximation is sampling.
Directly sampling from \(S_N\) has an obvious trivial algorithm with time complexity O(N). A further optimization is sampling from \(S_L, S_{L+1}, \dots, S_N\) together, which, when \(L \ll N\), reduces the amortized time complexity for each sample to O(1).
Hence, we derive the standard Chaos Game algorithm:
- Sample a point from \(S_0\).
- Iteratively choose one of transformations and apply it to the current point.
- Ignore the first \(L-1\) iterations, then keep the next \(N-L+1\) iterations.
Density Estimation
A common addition to getting the point set \(S\) is to estimate the probability density around each point, for a point set with density looks much nicer when visualized.
Conceptually, we additionally define a probability density function \(g\), and assign probability \(p_1, p_2, \dots, p_N\) to the transformations. Then \(g\) will be defined as:
$$
g(z)=\sum_{i=1}^N \frac{p(i) g(f_i(z))}{|J_{f_i}(z)|}
$$
And the corresponding chaos game is just also count the number of times each pixel is hit.
Note that the concept is used very loosely. The fractal point set \(S\) often has an area of zero and a Hausdorff dimension below two. I am not sure if the “probability density function” above actually makes much mathematical sense. But I think it illustrates the idea behind density estimation.
And, as part of standard procedure of computer graphics, gamma correction or other forms of tone mapping is then applied to the resultant grayscale image.
Color Estimation
The trace of the iterative process can be seen as making a series of N-ary choices, with the last one being the most significant. Correspondingly, the color index of such a trace can be defined as
$$
c=\sum_{i=1}^N \frac{2^i}{2^{N+1}} \cdot c_{\mathrm{choice}_i}
$$
Where \(c_i\) is a color index for each transformation within \([0, 1]\). The \(c\) for each iterative trace is a weighted average of such indices, and is therefore also within \([0, 1]\). Then, by applying any color-mapping function from \([0,1]\) to \([0,1]^3\), one can achieve a continuous-looking color. Colors of different traces to the same pixel are then averaged.
Note that this process is essentially arbitrary. There is nothing holy about using powers of 2 as weights, or using a linear representation as a color index. In essence, one can come up with any function from \(N^M\) to \([0,1]^3\) to color a fractal.
And if we try to “backport” this algorithm to the fixed-point definition, we can roughly say
$$
C(z)=\frac{1}{g(z)}\sum_{i=1}^N \frac{p(i) g(f_i(z)) \frac{c_i+C(f_i(z)}2}{|J_{f_i}(z)|}
$$
I think the formula is slightly cursed by its dependence on the already-cursed definition of \(g\), but hopefully it can still provide some insight.
Enforcing Symmetry
Symmetry, what is it good for?
Aesthetically, that’s just what we humans do. Each time a new generative algorithm appears, we repeat that old question. We ask for repetition, and we repeatedly ask for repetition, because we sense a beauty in repeating repetition.
Mathematically, symmetry is just the invariance under transformations. And IFS are the fixed points of the Hutchinson operator, or, the union of transformations. Needless to say, the two concepts are pretty compatible. It even raises the question, that why do people still want “symmetry” when it’s the whole point of IFS? Anyways, the symmetry present in typical IFS images is too subtle and divorced from the common definition of symmetry, so it is not unreasonable to ask for images with both the fractal self-similarity symmetry and the more conventional symmetry.
More formally, if you have a semigroup of symmetric transformations \(s_0, s_1, s_2, \dots, s_{K-1}\), and you wish your image to be invariant under each of these, and you already have a set of transformations \(f_1, \dots, f_N\) to draw a fractal, then you can construct a new set of transformations \(\{s_i \circ f_j\}\), with which you obtain a fractal set that obeys both your symmetry requirements and corresponds to the original fractal in a very loose sense (i.e., it’s a superset of the original fractal).
The simplest situation is those rotational and bilateral symmetries, where the symmetric transformations are all rigid, and their number finite. They do not mess with the density estimation or color estimation, and the straightforward implementation just works.
Softwares
Flam3
Flam3 (leetspeak of “flame”, obviously) is the result of all such development. It’s a command line tool to generate and render such images.
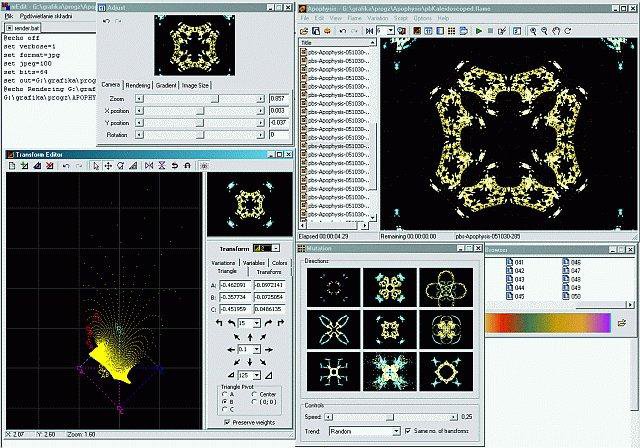
Apophysis
Apophysis gained fame around 2008. Then it was mostly abandoned. Anyways, it is one of the crash-prone programs that I still find worthy to run with wine, because there are few alternatives.
It provides a UI, so you can actually see the transformations and try out your ideas. It proves invaluable in my learning of the IFS.
Other abandoned projects
Flam4 was a CUDA-accelerated version of flam3.
Apophysis has numerous forks and plugins.
Fr0st was a PyWxGtk-based GUI for flam3/flam4.
Most of these were hosted on SourceForge, and I think both the fading interest in IFS and the mismanagement of SourceForge led to their abandonment.
References
The Fractal Flame Algorithm, formatted as a paper and included as part of the flam3 documentation, explains most of the basic ideas. However, it indulges in implementation details so much that one wants to question whether they cared about the general principle enough.